GIS基础(杂)：自相关/热点/异常分析，Moran's I和Gets-Ord Gi对比

发表于 2023-03-23 阅读次数： Waline：本文字数： 2.1k 阅读时长 ≈ 2 分钟

空间自相关强度计算、热点分析与异常值分析是空间分析中的常用工具，在此简单辨析一下空间自相关等相关工具的差异和用法。主要对比的是全局和局部的==Moran‘s I==以及==Getis-Ord General G==。

实际使用指南

方法的使用有前提假设，具体可以查看-参考
使用方法前，一定要明确分析的目标以及对应冷点热点或者聚集区的==物理含义及解释==
需要使用投影坐标系，单位为m或km
全局的Moran指数和Gets G都只能从整体上推断数据特征的空间分布，前者是判断随机还是分散还是聚集，当然，值的大小也可以指示强度；后者是给出高值或低值是否聚集，聚集程度。
对于距离阈值的判断可以采用遍历的方式寻找阈值，ArcGIS/Pro提供了工具增量空间自相关分析——寻找距离阈值，或者也可以使用R语言实现/Spatial Correlograms，此处的阈值也即是观测的尺度。
采用的是常用的Z-score进行统计显著性检验，因为只涉及单个数值的检验。

方法	尺度	用途	取值
Moran’s I	Global	整体上是聚集还是发散，也可以给出程度	-1，0，1
Getis-Ord Gi	Global	高低值聚集程度	>0
Local Moran's I	Local/逐对象	高/低值聚类探测，异常值分析	HH;LL;HJ;LH;不显著区（5类）
Getis-Ord Gi*	Local/逐对象	高/低值聚集区（热点区域）探测	±90 95 99%显著;不显著区（7类）

Global尺度

全局Moran’s I 是在假定均质的情况下给出变量总体自相关程度的统计量

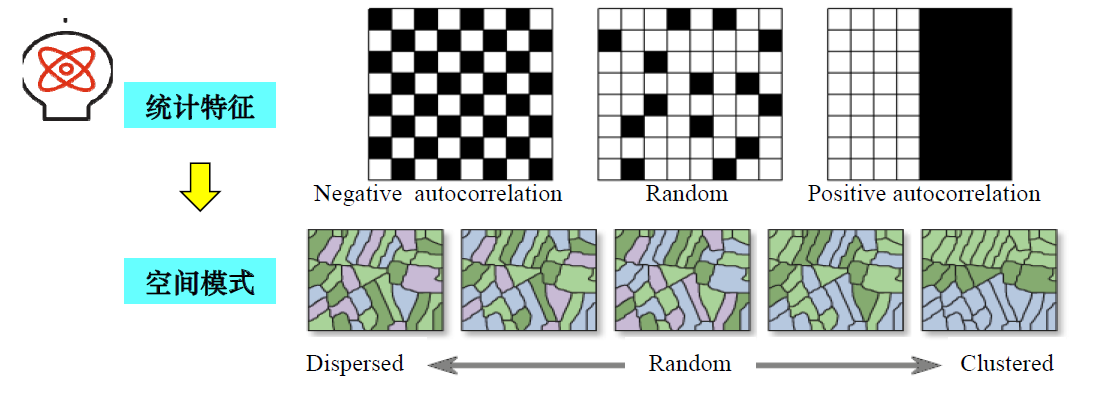
空间自相关(Spatial autocorrelation)，空间自相关用来刻画一个对象与其临近对象的相似程度。Moran’s I是用于推断变量“整体”的聚集程度，是倾向于聚集分布还是随机分布，而General G是判断变量中的“高值或低值”的聚集程度。

Moran’s I

Moran’s I衡量区域 (Global)尺度上某空间随机变量整体自相关的程度，这里比较的对象为==整体的均值==

通俗理解：协方差矩阵为正，代表“同方向变化”，为负则说明领域周围有的大于整体均值，有的比均值小。
Moran’s I 取值范围：[-1, 0, +1]，对应表明：负自相关-随机分布-正自相关，结果解释：
- 显著的==正==Z(+1.65, 单侧0.05)表明变量空间分布比期望的随机分布更加==聚集==(正相关)
- 显著的==负==Z( -1.65, 单侧0.05)表明变量空间分布比期望的随机分布更加==分散==(负相关)

Getis-Ord General G

Getis-Ord General G 是衡量区域(Global)尺度上某空间随机变量高值/低值的聚集程度的统计量, a measure of High/Low clustering。General G为正值>0，但对于一个二值(0/1)的wij来说，G取值[0, +1]

显著的==正==Z(+1.65, 单侧0.05)表明==高值==变量空间分布比期望的随机分布更加聚集
显著的==负==Z( -1.65, 单侧0.05)表明==低值==变量空间分布比期望的随机分布更加聚集

Local尺度——聚类及异常分析

以下两种方式的差异，具体可参考。简单来说，局部莫兰指数除了可以进行高低值聚类分析，还可以用于异常值分析，而Getis-Ord Gi* 则主要用于高高值或低低值的聚团发现，如下图我选一个区域，同时在30km的范围内计算二者的值，结果：

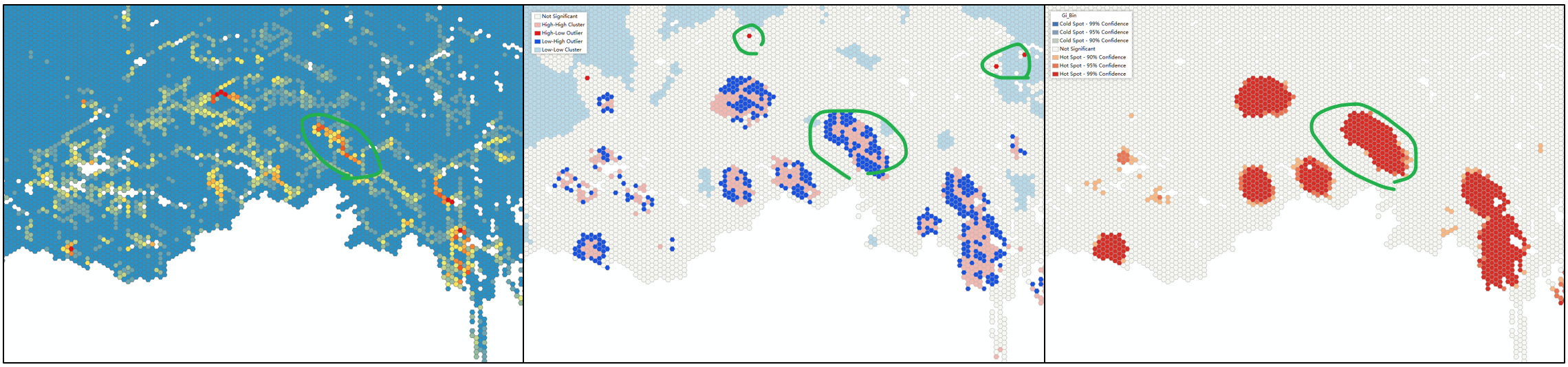
Local Moran’s I

实际上Moran’s I可以拆成n个Moran’s \(I_i\)的相乘，个体单元尺度上的空间自相关程度Local indicators of spatial association (LISA)。即使不存在显著的全局自相关/聚集，局部尺度也可能存在。对于每个对象，我们都计算它与周边对象的相似程度（周围的也都是高值还是都是低值，还是有高有低），注意，此处的高低是相对于全局均值而言。

解释：

显著的正Zi(+1.65, 单侧0.05)表明i单元与邻居有相似的值(高-高/低-低)-即聚集(Clusters)
显著的负Zi( -1.65, 单侧0.05)表明i单元与邻居有相异的值(高-低/低-高)-即异常(Outliers)
由此可以识别高-高(HH)和低-低(LL)聚集，以及高-低(HL)和低-高(LH)异常

Getis-Ord Gi*

高值对象很重要，但可能不是具有统计意义的热点。要成为统计上显着的热点，一个对象将具高值并且被其他高值对象包围。一个对象及其邻居的局部总和与所有对象的总和成比例地进行比较；当局部总和与预期的局部总和有很大差异时，并且当该差异太大以至于不是随机机会的结果时，会产生具有统计显着性的z 分数。

显著正 z 分数，z 分数越大，高值（热点）的聚类就越强烈
显著负 z 分数，z 分数越小，低值（冷点）的聚类就越强烈。