Numpy基础：ndarray的理解及其常用操作

发表于 分类于 阅读次数： Waline： 本文字数： 6.4k 阅读时长 ≈ 6 分钟

本笔记记录一下Numpy的一些基础，包括：（1）ndarray的数据结构及数值类型；（2）常见操作（Creation/Indexing/Reshaping/Broadcasting）的Quick References。学习资料

ndarray介绍

Numpy或Torch都是默认行优先的表达，详细可参考列或者行优先顺序存储

多维数组，由一段连续的内存块(contiguous block)+一个索引方案(indexing scheme)构成，也即实际底层的存储是一维结构，通过一定的方式索引映射为多维数组。

==视图和副本==（Views and copies）是Numpy中较为重要的概念，一些知识点：

  1. View：修改视图会同步修改原始数组，通过范围切片返回的是视图，如：a[2:10]返回a的一个视图
  2. Copy：修改副本不会导致源数据发生变化，如：a[1, 2, 3]，取值得到a的一个副本
    • 判断副本的方式.base is None：y = x[[1,2,3],:]; y.base is Noney is a copy
  3. 注意np.reshape()操作：当数据区域连续时，返回一个视图，否则返回一个副本
  4. 通过减少临时副本来节约内存，如下使用案例，通过out来避免中间数据的生成：
1
2
3
4
5
6
7
>>> X = np.ones(10, dtype=np.int)
>>> Y = np.ones(10, dtype=np.int)
>>> A = 2*X + 2*Y
# 修改为
>>> np.multiply(X, 2, out=X)
>>> np.multiply(Y, 2, out=Y)
>>> np.add(X, Y, out=X)
  1. 数据的偏移量==offsets==，步幅==strides==可用基于实际数组元素占用的字节数等来计算元素的位置，具体可以查阅相关的文档。

再谈视图

实际物理内存块的大小固定，但类型却==“可变”==，单个元素数据类型占用空间增大则元素个数变少-同理

有了上面的认识，我们就可以发现，ndarray中的数据类型不是固定的，取决于我们如何看待这片数据的内存区域，如，使用==ndarray.view()==，可以通过对内存区域不同的切割方式，来==完成数据类型的转换==，而无须对数据进行额外的copy，从而达到节约内存空间的目的。具体来说：y=x.view(np.byte): 将原本10×4Byte的空间(x是int型)，按照1Byte来解析，即40*1Byte，y与x数据共享同一内存区域，数据是相同的，只是解析数据的方式不同而已。

图像处理实例参考：当需要对输入图像三个通道进行相同的处理时，使用cv2.split和cv2.merge是相当浪费资源的，因为任何一个通道的数据对处理来说都是一样的，我们可以用view来将其转换为一维矩阵后再做处理，这要不需要额外的内存开销和时间开销。

1
2
3
4
5
def createFlatView(array):
    """Return a 1D view of an array of any dimensionality."""
    flatView = array.view()
    flatView.shape = array.size
    return flatView

Python代码向量化

思想：将原始的纯Python代码使用numpy的函数和思想来达到目的，并起到加快运算的目的。

如，通过Numpy的函数np.add()可用显著加快运算速度：

1
2
>>> [z1+z2 for (z1,z2) in zip(Z1,Z2)]
>>> np.add(Z1,Z2) # more faster

通过Numpy还能方便地得到常规运算不容易得到的结果，如使用np.add()计算嵌套列表的加法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def add_python(Z1,Z2):
    return [z1+z2 for (z1,z2) in zip(Z1,Z2)]
def add_numpy(Z1,Z2):
    return np.add(Z1,Z2)
# 原始的数据维度均为2*2
Z1 = [[1, 2], [3, 4]]
Z2 = [[5, 6], [7, 8]]
>>> Z1 + Z2
[[1, 2], [3, 4], [5, 6], [7, 8]] #4*2

>>> add_python(Z1, Z2)
[[1, 2, 5, 6], [3, 4, 7, 8]] # 2*4

>>> add_numpy(Z1, Z2) #2*2
[[ 6  8]
 [10 12]]

但需要注意的是:

  • 如果要保留这本书中的一条信息，那就是“过早的优化是万恶之源"。我们已经看到代码矢量化可以极大地改进您的计算，在某些情况下可以提高几个数量级。不过，问题向量化通常要强大得多。如果您在设计过程中过早编写代码矢量化，您将无法开箱即用，并且您肯定会错过一些真正强大的替代方案，因为您将无法正确识别您的问题我们已经在问题向量化章节中看到了。这需要一些经验，你必须要有耐心:经验不是一朝一夕的过程。
  • Numpy 是一个非常通用的库，但这并不意味着您必须在所有情况下都使用它。有的时候还有很多其他的可以使用的库。

速查手册

数据类型DataType

1
2
3
>>> x = np.array([1,2,3])
>>> x.dtype
dtype('int32')

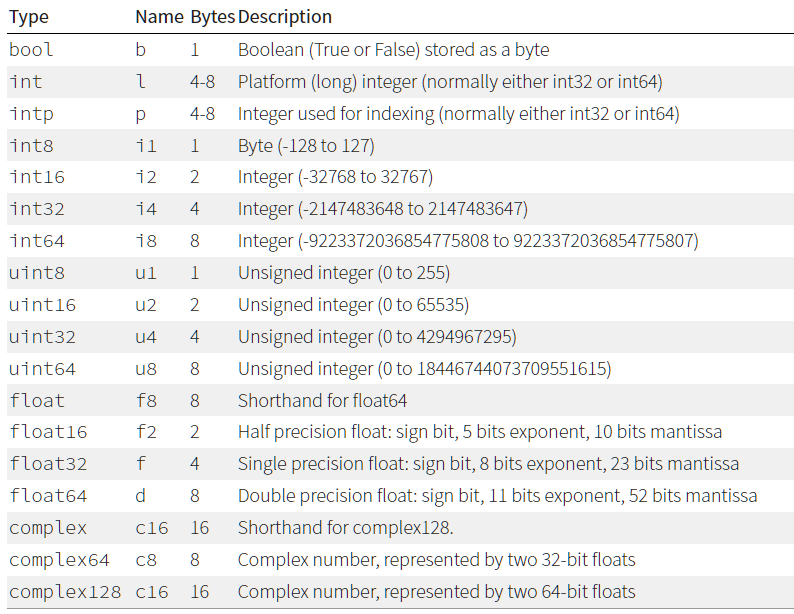
第一列为类型，第二列为简称，第三列为字节数、第四列为可以表达的数值范围

创建多维数组Creation

常见函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Z = np.zeros(9) # [0,0,0,0,0,0,0,0,0]
Z = np.ones(9)
Z = np.array([1,0,0,0,0,0,0,1,0])

Z = 2*np.ones(9)
>>> [2,2,2,2,2,2,2,2,2]

Z = np.arange(9)
>>> [0,1,2,...,8]
# 转成3行三列
Z = np.arange(9).reshape(3,3)

# 指定间隔生成
Z = np.linspace(0, 1, 5)
>>> [0.00, 0.25, 0.50, 0.75, 1.00]
# 创建格网
np.grid[0:3,0:3]

切片索引Indexing

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
Z = np.arange(9).reshape(3,3)
Z[0,0]
┏━━━┓───┬───┐   ┏━━━┓
┃ 0 ┃ 1 │ 2 │ → ┃ 0 ┃ (scalar)
┗━━━┛───┼───┤   ┗━━━┛
│ 3 │ 4 │ 5 │
├───┼───┼───┤
│ 6 │ 7 │ 8 │
└───┴───┴───┘
Z = np.arange(9).reshape(3,3)
Z[-1,-1]
┌───┬───┬───┐
│ 0 │ 1 │ 2 │
├───┼───┼───┤
│ 3 │ 4 │ 5 │
├───┼───┏━━━┓   ┏━━━┓
│ 6 │ 7 ┃ 8 ┃ → ┃ 8 ┃ (scalar)
└───┴───┗━━━┛   ┗━━━┛
Z = np.arange(9).reshape(3,3)
Z[1]
┌───┬───┬───┐
│ 0 │ 1 │ 2 │
┏━━━┳━━━┳━━━┓   ┏━━━┳━━━┳━━━┓
┃ 3 ┃ 4 ┃ 5 ┃ → ┃ 3 ┃ 4 ┃ 5 ┃
┗━━━┻━━━┻━━━┛   ┗━━━┻━━━┻━━━┛
│ 6 │ 7 │ 8 │      (view)
└───┴───┴───┘
Z = np.arange(9).reshape(3,3)
Z[:,2]
┌───┬───┏━━━┓   ┏━━━┓
│ 0 │ 1 ┃ 2 ┃   ┃ 2 ┃
├───┼───┣━━━┫   ┣━━━┫
│ 3 │ 4 ┃ 5 ┃ → ┃ 5 ┃ (view)
├───┼───┣━━━┫   ┣━━━┫
│ 6 │ 7 ┃ 8 ┃   ┃ 8 ┃
└───┴───┗━━━┛   ┗━━━┛
Z = np.arange(9).reshape(3,3)
Z[1:,1:]
┌───┬───┬───┐
│ 0 │ 1 │ 2 │    (view)
├───┏━━━┳━━━┓   ┏━━━┳━━━┓
│ 3 ┃ 4 ┃ 5 ┃   ┃ 4 ┃ 5 ┃
├───┣━━━╋━━━┫ → ┣━━━╋━━━┫
│ 6 ┃ 7 ┃ 8 ┃   ┃ 7 ┃ 8 ┃
└───┗━━━┻━━━┛   ┗━━━┻━━━┛
Z = np.arange(9).reshape(3,3)
Z[::2,::2]
┏━━━┓───┏━━━┓   ┏━━━┳━━━┓
┃ 0 ┃ 1 ┃ 2 ┃   ┃ 0 ┃ 2 ┃
┗━━━┛───┗━━━┛ → ┣━━━╋━━━┫
│ 3 │ 4 │ 5 │   ┃ 6 ┃ 8 ┃
┏━━━┓───┏━━━┓   ┗━━━┻━━━┛
┃ 6 ┃ 7 ┃ 8 ┃    (view)
┗━━━┛───┗━━━┛
Z = np.arange(9).reshape(3,3)
Z[[0,1],[0,2]]
┏━━━┓───┬───┐
┃ 0 ┃ 1 │ 2 │
┗━━━┛───┏━━━┓   ┏━━━┳━━━┓
│ 3 │ 4 ┃ 5 ┃ → ┃ 0 ┃ 5 ┃
├───┼───┗━━━┛   ┗━━━┻━━━┛
│ 6 │ 7 │ 8 │    (copy)
└───┴───┴───┘

Reshaping

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
Z = np.array([0,0,0,0,0,0,0,0,0,0,1,0])
┌───┬───┬───┬───┬───┬───┬───┬───┬───┬───┏━━━┓───┐
│ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │ 0 ┃ 1 ┃ 0 │
└───┴───┴───┴───┴───┴───┴───┴───┴───┴───┗━━━┛───┘
Z = np.array([0,0,0,0,0,0,0,0,0,0,1,0]).reshape(12,1)
┌───┐
│ 0 │
├───┤
│ 0 │
├───┤
│ 0 │
├───┤
│ 0 │
├───┤
│ 0 │
├───┤
│ 0 │
├───┤
│ 0 │
├───┤
│ 0 │
├───┤
│ 0 │
├───┤
│ 0 │
┏━━━┓
┃ 1 ┃
┗━━━┛
│ 0 │
└───┘
Z = np.array([0,0,0,0,0,0,0,0,0,0,1,0]).reshape(3,4)
┌───┬───┬───┬───┐
│ 0 │ 0 │ 0 │ 0 │
├───┼───┼───┼───┤
│ 0 │ 0 │ 0 │ 0 │
├───┼───┏━━━┓───┤
│ 0 │ 0 ┃ 1 ┃ 0 │
└───┴───┗━━━┛───┘
Z = np.array([0,0,0,0,0,0,0,0,0,0,1,0]).reshape(4,3)
┌───┬───┬───┐
│ 0 │ 0 │ 0 │
├───┼───┼───┤
│ 0 │ 0 │ 0 │
├───┼───┼───┤
│ 0 │ 0 │ 0 │
├───┏━━━┓───┤
│ 0 ┃ 1 ┃ 0 │
└───┗━━━┛───┘
Z = np.array([0,0,0,0,0,0,0,0,0,0,1,0]).reshape(6,2)
┌───┬───┐
│ 0 │ 0 │
├───┼───┤
│ 0 │ 0 │
├───┼───┤
│ 0 │ 0 │
├───┼───┤
│ 0 │ 0 │
├───┼───┤
│ 0 │ 0 │
┏━━━┓───┤
┃ 1 ┃ 0 │
┗━━━┛───┘
Z = np.array([0,0,0,0,0,0,0,0,0,0,1,0]).reshape(2,6)
┌───┬───┬───┬───┬───┬───┐
│ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │
├───┼───┼───┼───┏━━━┓───┤
│ 0 │ 0 │ 0 │ 0 ┃ 1 ┃ 0 │
└───┴───┴───┴───┗━━━┛───┘

广播Broadcasting

转变/扩充为相同纬度的ndarray再进行运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Z1 = np.arange(9).reshape(3,3)
Z2 = 1
>>> Z1 + Z2
┌───┬───┬───┐   ┌───┐   ┌───┬───┬───┐   ┏━━━┓───┬───┐   ┌───┬───┬───┐
│ 0 │ 1 │ 2 │ + │ 1 │ = │ 0 │ 1 │ 2 │ + ┃ 1 ┃ 1 │ 1 │ = │ 1 │ 2 │ 3 │
├───┼───┼───┤   └───┘   ├───┼───┼───┤   ┗━━━┛───┼───┤   ├───┼───┼───┤
│ 3 │ 4 │ 5 │           │ 3 │ 4 │ 5 │   │ 1 │ 1 │ 1 │   │ 4 │ 5 │ 6 │
├───┼───┼───┤           ├───┼───┼───┤   ├───┼───┼───┤   ├───┼───┼───┤
│ 6 │ 7 │ 8 │           │ 6 │ 7 │ 8 │   │ 1 │ 1 │ 1 │   │ 7 │ 8 │ 9 │
└───┴───┴───┘           └───┴───┴───┘   └───┴───┴───┘   └───┴───┴───┘
Z1 = np.arange(9).reshape(3,3)
Z2 = np.arange(3)[::-1].reshape(3,1)
>>> Z1 + Z2
┌───┬───┬───┐   ┌───┐   ┌───┬───┬───┐   ┏━━━┓───┬───┐   ┌───┬───┬───┐
│ 0 │ 1 │ 2 │ + │ 2 │ = │ 0 │ 1 │ 2 │ + ┃ 2 ┃ 2 │ 2 │ = │ 2 │ 3 │ 4 │
├───┼───┼───┤   ├───┤   ├───┼───┼───┤   ┣━━━┫───┼───┤   ├───┼───┼───┤
│ 3 │ 4 │ 5 │   │ 1 │   │ 3 │ 4 │ 5 │   ┃ 1 ┃ 1 │ 1 │   │ 4 │ 5 │ 6 │
├───┼───┼───┤   ├───┤   ├───┼───┼───┤   ┣━━━┫───┼───┤   ├───┼───┼───┤
│ 6 │ 7 │ 8 │   │ 0 │   │ 6 │ 7 │ 8 │   ┃ 0 ┃ 0 │ 0 │   │ 6 │ 7 │ 8 │
└───┴───┴───┘   └───┘   └───┴───┴───┘   ┗━━━┛───┴───┘   └───┴───┴───┘
Z1 = np.arange(9).reshape(3,3)
Z2 = np.arange(3)[::-1]
>>> Z1 + Z2
┌───┬───┬───┐   ┌───┬───┬───┐   ┌───┬───┬───┐   ┏━━━┳━━━┳━━━┓   ┌───┬───┬───┐
│ 0 │ 1 │ 2 │ + │ 2 │ 1 │ 0 │ = │ 0 │ 1 │ 2 │ + ┃ 2 ┃ 1 ┃ 0 ┃ = │ 2 │ 2 │ 2 │
├───┼───┼───┤   └───┴───┴───┘   ├───┼───┼───┤   ┗━━━┻━━━┻━━━┛   ├───┼───┼───┤
│ 3 │ 4 │ 5 │                   │ 3 │ 4 │ 5 │   │ 2 │ 1 │ 0 │   │ 5 │ 5 │ 5 │
├───┼───┼───┤                   ├───┼───┼───┤   ├───┼───┼───┤   ├───┼───┼───┤
│ 6 │ 7 │ 8 │                   │ 6 │ 7 │ 8 │   │ 2 │ 1 │ 0 │   │ 8 │ 8 │ 8 │
└───┴───┴───┘                   └───┴───┴───┘   └───┴───┴───┘   └───┴───┴───┘
Z1 = np.arange(3).reshape(3,1)
Z2 = np.arange(3).reshape(1,3)
>>> Z1 + Z2
┌───┐   ┌───┬───┬───┐   ┏━━━┓───┬───┐   ┏━━━┳━━━┳━━━┓   ┌───┬───┬───┐
│ 0 │ + │ 0 │ 1 │ 2 │ = ┃ 0 ┃ 0 │ 0 │ + ┃ 0 ┃ 1 ┃ 2 ┃ = │ 0 │ 1 │ 2 │
├───┤   └───┴───┴───┘   ┣━━━┫───┼───┤   ┗━━━┻━━━┻━━━┛   ├───┼───┼───┤
│ 1 │                   ┃ 1 ┃ 1 │ 1 │   │ 0 │ 1 │ 2 │   │ 1 │ 2 │ 3 │
├───┤                   ┣━━━┫───┼───┤   ├───┼───┼───┤   ├───┼───┼───┤
│ 2 │                   ┃ 2 ┃ 2 │ 2 │   │ 0 │ 1 │ 2 │   │ 2 │ 3 │ 4 │
└───┘                   ┗━━━┛───┴───┘   └───┴───┴───┘   └───┴───┴───┘