强化学习入门（2）

发表于 2023-11-17 分类于机器学习与深度学习阅读次数： Waline：本文字数： 4.4k 阅读时长 ≈ 4 分钟

学习task02，关于模型的建立和训练，免模型预测和控制，预测此处指学习环境的状态转移矩阵，控制则是得到并改进策略并输出最佳结果。

这一次的task方法的推导部分不少地方暂未走通，简单模型的搭建和运行未开展，后续填坑hh

免模型预测

https://johnjim0816.com/joyrl-book/#/ch4/main

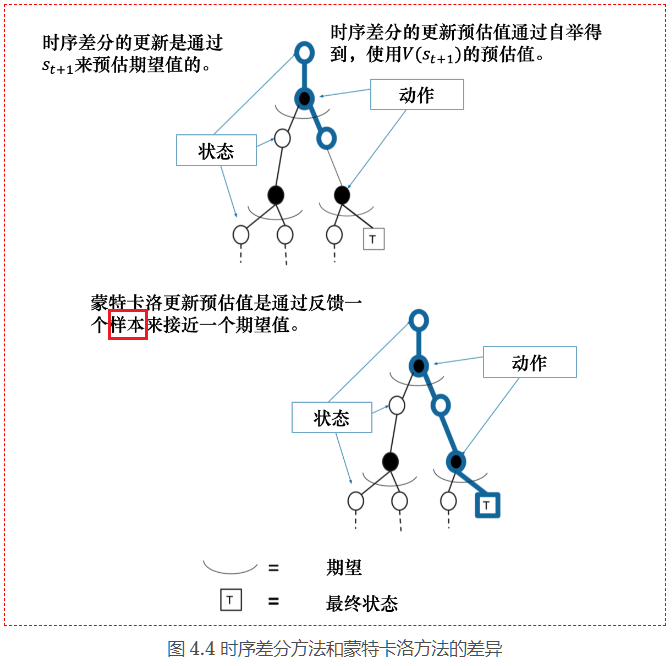
本章介绍常见的两种免模型预测方法，蒙特卡洛方法(MC)和时序差分方法(TD)。除动态规划之外，基础的强化学习算法都是免模型的。

有模型与免模型？预测与控制？

有模型强化学习指“有环境模型”的强化学习，即状态转移概率已知或预先学习到。优点是节约成本，可以在不与真实环境交互的情况下进行学习。
免模型则直接从与环境的交互中学习，在学习过程中需要与真实环境进行大量的交互。
预测：免模型事先不知道环境的状态转移概率，因此需要先去近似环境的状态价值函数——预测过程
控制：找到一个最优策略，过程通常涉及策略评估和策略改进

待预测的状态价值函数，最优策略、累积回报的期望： \[ \begin{aligned} V_\pi(s) & =\mathbb{E}_\pi\left[R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots \mid S_t=s\right] \\ & =\mathbb{E}_\pi\left[G_t \mid S_t=s\right] \end{aligned} \]

蒙特卡洛模拟估计

一种统计模拟方法，通过多次重复的采样观测来逼近实际状态价值函数

蒙特卡洛方法的思路是我们可以采样大量的轨迹，对于每个轨迹计算对应状态的回报然后取平均近似，称之为经验平均回报。根据大数定律，只要采样的轨迹数量足够多，计算出的经验平均回报就能趋近于实际的状态价值函数。
蒙特卡洛方法有一定的局限性，即只适用于有终止状态的马尔可夫决策过程。

显然，当可能的状况和情况很多的情况下不能直接暴力模拟，实际使用主要包括两种，首次访问蒙特卡洛和每次访问蒙特卡洛。

FVMC，先模拟一个完整的回合，然后走一遍t并计算每个状态的回报，只在第一次遍历到某个状态时会记录并计算对应的回报
EVMC，每次经过计算都会会记录状态的回报
FVMC 是一种基于回合的增量式方法，具有无偏性和收敛快的优点，但是在状态空间较大的情况下，依然需要训练很多个回合才能达到稳定的结果。而 EVMC 则是更为精确的预测方法，但是计算的成本相对也更高。

估计值的迭代更新：新的估计值<---旧的估计值+步长×（目标值-旧的估计值），表达为公式如下，此处的\(\alpha\)相当于深度学习中的学习率，G-V即为回报估计的误差error。 \[ V\left(s_t\right) \leftarrow V\left(s_t\right)+\alpha\left[G_t-V\left(s_t\right)\right] \]

时序差分估计

一种基于经验的动态规划方法，它结合了蒙特卡洛和动态规划的思想。

奖励更新过程中使用了当前奖励和后继状态的估计，因此终止状态需要单独考虑
0步自举（bootstrap）——\(TD(0)\)：使用一个状态的估计值来更新该状态的估计值，没有再利用后续状态信息，\(r_{t+1}-V\left(s_t\right)\)

\[ \begin{cases}V\left(s_t\right) \leftarrow V\left(s_t\right)+\alpha\left[r_{t+1}-V\left(s_t\right)\right] & \text { 对于终止状态 } V\left(s_t\right) \\ V\left(s_t\right) \leftarrow V\left(s_t\right)+\alpha\left[r_{t+1}+\gamma V\left(s_{t+1}\right)-V\left(s_t\right)\right] & \text { 对于非终止状态 } V\left(s_t\right)\end{cases} \] n 步时序差分:时序差分方法进一步拓展，自举的步数从0步拓展到n步

和蒙特卡洛的联系：趋近无穷时，就变成了蒙特卡洛方法，因此可以通过调整n实现两种方法的权衡
这个\(n\)值具体情况需要具体选取和实验，常见方法：网格搜索、随机搜索、训练自适应选择、交叉验证、经验取值

两种方法的比较

时序差分效率更高，受条件的限制更少更灵活，且在马尔可夫环境下有更高的学习效率

效率：时序差分方法可以在线学习，每走一步就可以更新，效率高。蒙特卡洛方法必须等游戏结束时才可以学习。
时序差分方法可以从不完整序列上进行学习。蒙特卡洛方法只能从完整的序列上进行学习。
时序差分方法可以在连续的环境下（没有终止）进行学习。蒙特卡洛方法只能在有终止的情况下学习。
时序差分方法利用了马尔可夫性质，在马尔可夫环境下有更高的学习效率。蒙特卡洛方法没有假设环境具有马尔可夫性质，利用采样的价值来估计某个状态的价值，在不是马尔可夫的环境下更加有效。

免模型控制

控制，即给定一个马尔可夫决策过程，输出最优策略以及对应的最优价值函数

Q-learning 算法

强化学习训练过程

首先我们会迭代很多个回合，在每回合中，首先重置环境回到初始化的状态，智能体根据状态选择动作，然后环境反馈中下一个状态和对应的奖励，同时智能体会更新策略，直到回合结束。

for i_ep in range(train_eps): # 遍历每个回合
    # 重置环境，获取初始状态
    state = env.reset()  # 重置环境,即开始新的回合
    while True: # 对于比较复杂的游戏可以设置每回合最大的步长，例如while ep_step<100，即最大步长为100。
        # 智能体根据策略采样动作
        action = agent.sample_action(state)  # 根据算法采样一个动作
        # 与环境进行一次交互，得到下一个状态和奖励
        next_state, reward, terminated, _ = env.step(action)  # 智能体将样本记录到经验池中
        agent.memory.push(state, action, reward, next_state, terminated) 
        # 智能体更新策略
        agent.update(state, action, reward, next_state, terminated)  
        # 更新状态
        state = next_state  
        # 如果终止则本回合结束
        if terminated:
            break

强化学习中有几个要素，智能体、环境、经验池（经回放），还要考虑一下智能体在强化学习中主要负责哪些工作。

定义智能体

采样动作

class Agent:
    def __init__():
        pass
    def sample_action(self, state):
        ''' 采样动作，训练时用
        '''
        self.sample_count += 1
        # epsilon是会递减的，这里选择指数递减
        self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * math.exp(- self.sample_count / self.epsilon_decay) 
        # e-greedy 策略
        if np.random.uniform(0, 1) > self.epsilon:
            action = np.argmax(self.Q_table[str(state)]) # 选择Q(s,a)最大对应的动作
        else:
            action = np.random.choice(self.n_actions) # 随机选择动作
        return action

预测动作，测试不需要额外探索，直接输出Q值对应最大的动作

class Agent:
    def __init__():
        pass
    def predict_action(self,state):
        ''' 预测或选择动作，测试时用
        '''
        action = np.argmax(self.Q_table[str(state)])
        return action

更新方法

def update(self, state, action, reward, next_state, terminated):
    Q_predict = self.Q_table[str(state)][action] 
    if terminated: # 终止状态
        Q_target = reward  
    else:
        Q_target = reward + self.gamma * np.max(self.Q_table[str(next_state)]) 
    self.Q_table[str(state)][action] += self.lr * (Q_target - Q_predict)

定义环境

当然大多数情况下需要根据需求建立我们自己的环境，这时我们也可以仿照 Gym 的模式来做

我们选择的环境是 OpenAI Gym 开发的，它提供了一套标准化的环境，包括经典的控制理论问题和游戏，代码封装得也比较好，只需要一行代码就能定义好环境，如下：

1	env = gym.make('CliffWalking-v0')

获取环境的状态数和动作数

n_states = env.observation_space.n # 状态数
n_actions = env.action_space.n # 动作数
print(f"状态数：{n_states}， 动作数：{n_actions}")

设参数

Q-learning 算法的超参数（需要人工调整的参数）比较少，其中折扣因子比较固定，设置在 0.9 到 0.999 之间，一般设置成 0.99 即可。而学习率在本章节中设置的比较大，为 0.1，实际更复杂的环境和算法中学习率是小于 0.01，因为太大很容易发生过拟和的问题，只是本节的环境和算法都比较简单，为了收敛得更快点所以设置得比较大。此外由于我们探索策略中的\(\epsilon\)是会随着采样步数衰减的，在实践过程中既不能让它衰减得太快也不能让它衰减得太慢，因此需要合理设置如下参数：

1
2
3

self.epsilon_start = 0.95 #  e-greedy策略中epsilon的初始值
self.epsilon_end = 0.01 #  e-greedy策略中epsilon的最终值
self.epsilon_decay = 200 #  e-greedy策略中epsilon的衰减率

开始训练并分析结果

Q-learning

Sarsa